Steve Mann
[email protected]
http://wearcam.org/mann.html
University of Toronto, Department of Electrical and Computer Engineering,
10 King's College Road, Room 2001,
Toronto, Ontario, Canada, M5S 3G4
Tel. (416) 946-3387, Fax. (416) 971-2326
Humanistic Intelligence (HI) is proposed as a new signal processing framework in which the processing apparatus is inextricably intertwined with the natural capabilities of our human body and mind. Rather than trying to emulate human intelligence, HI recognizes that the human brain is perhaps the best neural network of its kind, and that there are many new signal processing applications, within the domain of personal technologies, that can make use of this excellent but often overlooked processor. The emphasis of this paper is on personal imaging applications of HI, as we take a first step toward an intelligent wearable camera system that can allow us to effortlessly capture our day-to-day experiences, help us remember and see better, provide us with personal safety through crime reduction, and facilitate new forms of communication through collective connected humanistic intelligence. The wearable signal processing hardware, which began as a cumbersome backpack-based photographic apparatus of the 1970s, and evolved into a clothing-based apparatus in the early 1980s, currently provides the computational power of a UNIX workstation concealed within ordinary-looking eyeglasses and clothing. Thus it may be worn continuously during all facets of ordinary day-to-day living, so that, through long-term adaptation, it begins to function as a true extension of the mind and body.
Introduction
What is now proposed, is a new form of ``intelligence''
whose goal is to not only work in close synergy with the human
user, rather than as a separate entity, but more importantly,
to arise, in part, because of the very existence of the human user.
This close synergy is achieved through a
user-interface
to signal processing hardware that is both in
close physical proximity
to the user, and is
constant.
By constant, what is meant is that the apparatus is
both interactionally and operationally constant.
This constancy of user-interface separates this signal processing architecture from other related devices such as pocket calculators and Personal Data Assistants (PDAs).
By operationally constant, what is meant is that although it may have ``sleep" modes, it is never ``dead" (as is typically a calculator which may be worn in a shirt pocket). By interactionally constant, what is meant is that the inputs and outputs of the device are always potentially active. Thus, for example, a pocket calculator, worn in a shirt pocket, and left on all the time is still not interactionally constant, because it cannot be used in this state (e.g. one still has to pull it out of the pocket to see the display or enter numbers). A wrist watch is a borderline case. Although it continues to keep proper time, and it is worn on the body, one must make a conscious effort to orient it within one's field of vision.
Why HI? It is not, at first, obvious why one might want devices such as pocket calculators to be operationally constant. However, we will later see why it is desirable to have certain personal electronics devices, such as cameras and signal processing hardware, be on constantly, for example, to facilitate new forms of intelligence that assist the user in new ways.
Devices embodying humanistic intelligence are not merely intelligent signal processors that a user might wear or carry in close proximity to the body, but instead, are devices that turn the user into part of an intelligent control system where the user becomes an integral part of the feedback loop.
HI does not necessarily mean ``user-friendly'' Devices embodying HI often require that the user learn a new skill set, and are therefore not necessarily easy to learn. Just as it takes a young child many years to become proficient at using his or her hands, some of the devices that implement HI have taken years of use before they began to truly behave as if they were natural extensions of the mind and body. Thus, in terms of Human-Computer Interactionbaecker87all, the goal is not just to construct a device that can model (and learn from) the user, but, more importantly, to construct a device in which the user also must learn from the device. Therefore, in order to facilitate the latter, devices embodying HI should provide a constant user-interface -- one that is not so sophisticated and intelligent that it confuses the user. Although the device may implement very sophisticated signal processing algorithms, the cause and effect relationship of this processing to its input (typically from the environment or the user's actions) should be clearly and continuously visible to the user, even when the user is not directly and intentionally interacting with the apparatus. Accordingly, the most successful examples of HI afford the user a very tight feedback loop of system observability (ability to perceive how the signal processing hardware is responding to the environment), even when the controllability of the device is not engaged (e.g. at times when the device is not being used). A simple example is the viewfinder of a wearable camera system, which provides framing, a photographic point of view, and facilitates to the user a general awareness of the visual effects of the camera's own image processing algorithms, even when pictures are not being taken. Thus the human operator is always in the feedback loop of the imaging process, even though pictures may only be taken occasionally. A more sophisticated example is the biofeedback-controlled wearable camera system, in which the biofeedback process happens continuously, whether or not a picture is actually being taken. In this sense, the user becomes one with the machine, over a long period of time, even if the machine is only ``used'' (e.g. to actually take a picture) occasionally.
HI attempts to both build upon, as well as re-contextualize, concepts in intelligent signal processinghaykinneural[4], and related concepts such as neural networkshaykinneural[5][6], fuzzy logickoskofuzzy[8], and artificial intelligenceminsky60. HI also suggests a new goal for signal processing hardware, that is, to directly assist, rather than replace or emulate human intelligence. What is needed to facilitate this vision is a simple computational signal processing framework that empowers the human intellect.
`WearComp' as means of realizing HI
WearCompmannieeecomputer is now proposed as an apparatus
upon which a practical realization of HI can be built,
as well as a research tool for new studies in intelligent
signal
processing.
The apparatus consists of a battery-powered wearable
Internet-connectedmanncq-vhf computer
system with miniature
eyeglass-mounted screen and appropriate optics
to form the virtual image equivalent to an ordinary desktop
multimedia computer. However, because the apparatus is tetherless,
it travels with the user, presenting a computer screen that
either appears superimposed on top of the real world,
or represents the real world as a video image[12].
Due to advances in low power microelectronicsmeindl, we are entering a pivotal era in which it will become possible for us to be inextricably intertwined with computational technology that will become part of our everyday lives in a much more immediate and intimate way than in the past.
Physical proximity and constancy were
simultaneously realized by the `WearComp'
project
of the 1970s and early 1980s (Figure 1)
Figure 1: Early embodiments of the author's original
``photographer's assistant'' application
of Personal Imaging. (a) Author wearing WearComp2, an early 1980s
backpack-based signal processing and personal imaging
system with right eye
display. Two antennas operating at different frequencies
facilitated wireless communications over a full-duplex
radio link.
(b) WearComp4, a late 1980s clothing-based signal processing
and personal imaging
system with left eye display and beam splitter.
Separate antennas
facilitated simultaneous voice, video, and data communication.
which was a first attempt at building an intelligent ``photographer's assistant'' around the body, and comprised a computer system attached to the body, a display means constantly visible to one or both eyes, and means of signal input including a series of pushbutton switches and a pointing device (Fig 2)
Figure 2: Author using
some early
input devices (``keyboards'' and ``mice'') for WearComp:
(a) 1970s: input device comprising pushbutton switches
mounted to a wooden hand-grip
(b) 1980s: input device
comprising microswitches mounted to the handle of an
electronic flash. These devices also incorporated a
detachable joystick (controlling two potentiometers),
designed as a pointing device for use in conjunction with
the WearComp project.
that the wearer could hold in one hand to function as a keyboard and mouse do, but still be able to operate the device while walking around. In this way, the apparatus re-situated the function to a desktop multimedia computer with mouse, keyboard, and video screen, as a physical extension of the user's body. While size and weight reduction of WearComp over the last 20 years (from WearComp0 to WearComp8) have been quite dramatic, the basic qualitative elements and functionality have remained essentially the same, apart from the obvious increase in computational power.
However, what makes WearComp particularly useful in new and interesting ways, and what makes it particularly suitable as a basis for humanistic intelligence, is the collection of other input devices, not all of which are found on a desktop multimedia computer.
In typical embodiments of `WearComp' these measurement (input) devices include the following:
Certain applications use only a subset of these devices, but including all of them in the design facilitates rapid prototyping and experimentation with new applications. Most embodiments of WearComp are modular, so that devices can be removed when they are not being used.
A side-effect of this `WearComp' apparatus is that it replaces much of the personal electronics that we carry in our day-to-day living. It enables us to interact with others through its wireless data communications link, and therefore replaces the pager and cellular telephone. It allows us to perform basic computations, and thus replaces the pocket calculator, laptop computer and personal data assistant (PDA). It can record data from its many inputs, and therefore it replaces and subsumes the portable dictating machine, camcorder, and the photographic camera. And it can reproduce (``play back'') audiovisual data, so that it subsumes the portable audio cassette player. It keeps time, as any computer does, and this may be displayed when desired, rendering a wristwatch obsolete. (A calendar program which produces audible, vibrotactile, or other output also renders the alarm clock obsolete.)
However, it goes beyond replacing all of these items, because not only is it currently far smaller and far less obtrusive than the sum of what it replaces, but these functions are interwoven seamlessly, so that they work together in a mutually assistive fashion. Furthermore, entirely new functionalities, and new forms of interaction arise, such as enhanced sensory capabilities, as will be discussed in Sections 3 and 4. Underwearables The wearable signal processing apparatus of the 1970s and early 1980s was cumbersome at best, so an effort was directed toward not only reducing its size and weight, but, more importantly, reducing its undesirable and somewhat obtrusive appearance, as well as making an apparatus of a given size and weight more comfortable to wear and bearable to the usermannieeecomputer. It was foundmannpithesis that the same apparatus could be made much more comfortable by bringing the components closer to the body which had the effect of reducing both the torque felt bearing the load, as well as the moment of inertia felt in moving around. This effort resulted in a version of WearComp called the `Underwearable Computer'mannpithesis shown in Figure 3.
Figure 3: The `underwearable' signal processing hardware:
(a) as worn by author (b) close up showing webbing for routing of cabling.
Typical embodiments of the underwearable resemble an athletic undershirt (tank top) made of durable mesh fabric, upon which a lattice of webbing is sewn. This facilitates quick reconfiguration in the layout of components, and re-routing of cabling. Note that wire ties are not needed to fix cabling, as it is simply run through the webbing, which holds it in place. All power and signal connections are standardized, so that devices may be installed or removed without the use of any tools (such as soldering iron) by simply removing the garment and spreading it out on a flat surface.
Some more recent related work by others lind97, also involves building circuits into clothing, in which a garment is constructed as a monitoring device to determine the location of a bullet entry. The underwearable differs from this monitoring apparatus in the sense that the underwearable is totally reconfigurable in the field, and also in the sense that it embodies humanistic intelligence (the apparatus reported in lind97 performs a monitoring function but does no facilitate human interaction).
In summary, there were three reasons for the signal processing hardware being `underwearable':
Figure 4: Covert embodiments of WearComp suitable for
use in ordinary day-to-day situations.
Both incorporate fully functional UNIX-based computers
concealed in the small of the back, with the rest of
the peripherals, analog to digital converters, etc.,
also concealed under ordinary clothing.
Both incorporate cameras concealed within the eyeglasses,
the importance of which will become evident in Section 3,
in the context of Personal Imaging.
(a) lightweight black and white version completed in
1995. This is also an ongoing project (e.g.
implementation of full-color system in same size,
weight, and degree of concealment is expected in 1998).
(b) full-color version completed in 1996
included special-purpose digital signal processing
hardware based on an array of TMS 320 series
processors connected to a UNIX-based host processor,
concealed in the back of the underwearable.
The cross-compiler for the TMS 320 series chips
was run remotely on a SUN workstation, accessed
wirelessly through radio and
antennas concealed in the apparatus.
Smart clothing: building signal-processing devices directly into fabric
Starting in 1982, Eleveld and Mann[15] began an effort to build circuitry into clothing. The term `smart clothing' refers to variations of WearComp that are built directly into clothing, and are characterized by (or at least an attempt at) making components distributed rather than lumped, whenever possible or practical.
Smart clothing was inspired by the need for comfortable signal processing devices that could be worn for extended periods of time. The inspiration for smart clothing arose out of noticing that some of the early headsets typically used with ``crystal radios'' were far more comfortable than the newer headsets, and could often be worn for many hours (some such early headsets had no head bands but instead was sewn into a cloth cap meant to be worn underneath a helmet). Of particular interest was the cords used in some of the early headsets (Fig 5(a)), early telephones, early patch cords,
Figure 5: Some simple examples of cloth which has been rendered
conductive.
(a) Cords on early headsets, telephones, etc., often felt more
like rope than wire.
(b) A recent generation of
conductive clothing made from bridged-conductor
two-waymannhistorical (BC2) fabric.
Although manufactured to address the growing concerns
regarding exposure to electromagnetic
radiation a, such conductive fabric may be used
to shield signal processing circuits from interference.
Signal processing circuits worn underneath such garments
were found to function much better due to this shielding.
This outerwear functions as a faraday cage for the
underwearable computing.
etc., which were much more like rope than like wire.
The notion that cloth be rendered conductive, through the addition of metallic fibers interwoven into it, is one thing that makes possible clothing that serves as an RF shield (Fig 5(b)), manufactured to address response to the growing fear of the health effects of long-term exposure to radio-frequency exposurecybercap. However, it may also be used to shield signal processing circuits from outside interference, or as a ground plane for various forms of conformal antennas sewn into the clothing[14].
Smart clothing is made using either of the following two approaches:
Conductive materials have been used in certain kinds of drapery for many years for appearance and stiffness, rather than electrical functionality, but these materials can be used to make signal processing circuits, as depicted in Figure 6. Simple circuits like this suggest a future possible direction for research in this area.
Figure 6: Signal processing with
`smart clothing'.
(a) Portion of a circuit diagram showing the new notation
developed to denote four L.E.D. indicators and some
comparators.
The ``X'' and ``O'' notation borrows from the tradition of
depicting arrows in and out of the page (e.g. ``X'' denotes
connection to top layer which is oriented in the up-down
direction, while ``O'' denotes connection to bottom ``across''
layer).
The ``sawtooth'' denotes a cut line where enough of the fabric
is removed that the loose ends will not touch.
Optional lines were drawn all the way from top to
bottom (and dotted or hidden lines across) to make it
easier to read the diagram.
(b) Four kinds of conductive fabric.
(c) Back of a recent article of smart clothing showing a solder joint
strengthened with a blob of glue).
Note the absence of wires leading to or from the glue blob,
since the fabric itself carries the electrical current.
(d) Three LEDs on type-BC1 fabric, bottom two lit, top one off.
(e) A signal processing shirt with LEDs as its display
medium. This apparatus was made
to pulse to the
beat of the wearer's heart
as a personal status monitor, or to music,
as an interactive fashion accessory.
This trivial but illustrative example of simple clothing-based
signal processing suggests the possibility of turning the more
useful devices that will be described in Sections 3 and 4
of this paper into ordinary clothing.
(C) Steve Mann, 1985;
thanks to Renatta Barrera for assistance.
Multidimensional signal input for HI
The close physical proximity of WearComp to the body, as described earlier,
facilitates a new form of signal
processing.
Because the apparatus is in direct contact with the body, it may
be equipped with various sensory devices.
For example, a tension transducer (pictured leftmost,
running the height of the picture from top to bottom, in
Fig 7).
is typically threaded through
and around the underwearable, at stomach height, so that it measures
respiration. Electrodes are also installed in such a manner that
they are in contact with the wearer's heart.
Various other sensors, such as an array of transducers in each
shoemannpt and a wearable radar
system (described in Section 4) are also included as sensory inputs
to the processor.
The ProComp 8 channel analog to digital converter with some of the
input devices that are sold with it is pictured in Fig 7
together with the CPU from WearComp6.
Figure 7:
Author's Personal Imaging system equipped with sensors
for measuring biological signals. The sunglasses
in the upper right are
equipped with built in video cameras and
display system. These look like ordinary sunglasses when
worn (wires are concealed inside the eyeglass holder).
At the left side of the picture is an 8 channel
analog to digital converter
together with a collection of biological sensors,
both manufactured by Thought Technologies Limited, of Canada.
At the lower right is an input device called the ``twiddler'',
manufactured by HandyKey, and to the left of that is a
Sony Lithium Ion camcorder battery with custom-made
battery holder. In the lower central area of the image is the
computer, equipped with special-purpose video processing/video
capture hardware (visible as the top stack on this stack of
PC104 boards). This computer, although somewhat bulky,
may be concealed in the small of the back, underneath
an ordinary sweater.
To the left of the computer, is a serial to
fiber-optic converter that provides communications to the
8 channel analog to digital converter over a fiber-optic link.
Its purpose is primarily one of safety, to isolate
high voltages used in the computer and peripherals
(e.g. the 500 volts or so present in the sunglasses)
from the biological sensors which are in close proximity,
typically with very good connection, to the body of the wearer.
It is important to realize that this apparatus is not merely a biological signal logging device, as is often used in the medical community, but, rather, enables new forms of real-time signal processing for humanistic intelligence. A simple example might include a biofeedback-driven video camera.
Picard also suggests its possible use to estimate human emotionpicard97.
The emphasis of this paper will be on visual image processing with the WearComp apparatus. The author's dream of the 1970s, that of an intelligent wearable image processing apparatus, is just beginning to come to fruition.
The Personal Imaging application of Humanistic Intelligence Some simple illustrative examples Always Ready: From point and click to `look and think'Current day commercial personal electronics devices we often carry are just useful enough for us to tolerate, but not good enough to significantly simplify our lives. For example, when we are on vacation, our camcorder and photographic camera require enough attention that we often either miss the pictures we want, or we become so involved in the process of video or photography that we fail to really experience the immediate present environmentnorman92.
One ultimate goal of the proposed apparatus and methodology is to ``learn" what is visually important to the wearer, and function as a fully automatic camera that takes pictures without the need for conscious thought or effort from the wearer. In this way, it might summarize a day's activities, and then automatically generate a gallery exhibition by transmitting desired images to the World Wide Web, or to specific friends and relatives who might be interested in the highlights of one's travel. The proposed apparatus, a miniature eyeglass-based imaging system, does not encumber the wearer with equipment to carry, or with the need to remember to use it, yet because it is recording all the time into a circular buffermannpithesis, merely overwriting that which is unimportant it is always ready. Thus, when the signal processing hardware detects something that might be of interest, recording can begin in a retroactive sense (e.g. a command may be issued to start recording from thirty seconds ago), and the decision can later be confirmed with human input. Of course this apparatus raises some important privacy questions which are beyond the scope of this article, but have been addressed elsewhere in the literaturemannacmmm96[23].
The system might use the inputs from the biosensors on the body, as a multidimensional feature vector with which to classify content as important or unimportant. For example, it might automatically record a baby's first steps, as the parent's eyeglasses and clothing-based intelligent signal processor make an inference based on the thrill of the experience. It is often moments like these that we fail to capture on film: by the time we find the camera and load it with film, the moment has passed us by.
Personal safety device for reducing crime A simple example of where it would be desirable that the device operate by itself, without conscious thought or effort, is in an extreme situation such as might happen if the wearer were attacked by a robber wielding a shotgun, and demanding cash.
In this kind of situation, it is desirable that the apparatus would function autonomously, without conscious effort from the wearer, even though the wearer might be aware of the signal processing activities of the measuring (sensory) apparatus he or she is wearing.
As a simplified example of how the processing might be done,
we know that the wearer's heart rate, averaged over a sufficient time window,
would likely increase
dramatically
with no corresponding increase in footstep rate
(in fact footsteps would probably slow at the request of the gunman).
The computer would then make an inference from the data, and predict a
high visual saliency. (If we simply take heart rate divided by
footstep rate, we can get a first-order approximation of the visual
saliency index.) A high visual saliency would trigger recording from
the wearer's camera at maximal frame rate, and also send
these images together with appropriate messages to
friends and relatives who would look at the images to determine whether
it was a false alarm or real danger.
Such a system is, in effect, using the wearer's brain as part of its processing pipeline, because it is the wearer who sees the shotgun, and not the WearComp apparatus (e.g. a much harder problem would have been to build an intelligent machine vision system to process the video from the camera and determine that a crime was being committed). Thus humanistic intelligence (intelligent signal processing arising, in part, because of the very existence of the human user) has solved a problem that would not be possible using machine-only intelligence.
Furthermore, this example introduces the concept of `collective connected humanistic intelligence', because the signal processing systems also rely on those friends and relatives to look at the imagery that is wirelessly send from the eyeglass-mounted video camera and make a decision as to whether it is a false alarm or real attack. Thus the concept of HI has become blurred across geographical boundaries, and between more than one human and more than one computer.
The retro-autofocus example: Human in the signal processing loop The above two examples dealt with systems which use the human brain, with its unique processing capability, as one of their components, in a manner in which the overall system operates without conscious thought or effort. The effect is to provide a feedback loop of which subconscious or involuntary processes becomes an integral part.
An important aspect of HI is that the conscious will of the user may be inserted into or removed from the feedback loop of the entire process at any time. A very simple example, taken from everyday experience, rather than another new invention, is now presented.
One of the simplest examples of HI is that which happens with some of the early autofocus Single Lens Reflex (SLR) cameras in which autofocus was a retrofit feature. The autofocus motor would typically turn the lens barrel, but the operator could also grab onto the lens barrel while the autofocus mechanism was making it turn. Typically the operator could ``fight'' with the motor, and easily overpower it, since the motor was of sufficiently low torque. This kind of interaction is particularly useful, for example, when shooting through a glass window at a distant object, where there are two or three local minima of the autofocus error function (e.g. focus on particles of dust on the glass itself, focus on a reflection in the glass, and focus on the distant object). Thus when the operator wishes to focus on the distant object and the camera system is caught in one of the other local minima (for example, focused on the glass), the user merely grasps the lens barrel, swings it around to the approximate desired location (as though focusing crudely by hand, on the desired object of interest), and lets go, so that the camera will then take over and bring the desired object into sharp focus.
This very simple example illustrates a sort of humanistic intelligent signal processing in which the intelligent autofocus electronics of the camera work in close synergy with the intellectual capabilities of the camera operator.
It is this aspect of HI, that allows the human to step into and out of the loop at any time, that makes it a powerful paradigm for intelligent signal processing.
Mathematical framework for personal imaging The theoretical framework for HI is based on processing a series of inputs from various wearable sensory apparatus, in a manner that regards each one of these as belonging to a measurement space; each of the inputs (except for the computer's ``keyboard'') is regarded as a measurement instrument to be linearized in some meaningful physical quantity.
Since the emphasis of this paper is on personal imaging, the treatment here will focus on the wearable camera (discussed here in Section 3) and the wearable radar (discussed in Section 4). The other measurement instruments are important, but their role is primarily to facilitate exploiting the human intellect for purposes of processing data from the imaging apparatus.
The theoretical framework for processing video
is based on regarding the camera as an array of light measuring
instruments capable of measuring
how the scene or objects in view of the camera
respond to light
This framework has two important special cases, the
first of which is based on photometric self-calibration to
build a lightspace map from images which differ only in overall exposure,
and the second of which is based on algebraic projective geometry
as a means of combining information from images
related to one-another by a projective coordinate transformation.
These two special cases of the theory are now presented in Sections 3.2.1 and 3.2.2 respectively, followed by bringing both together in Section 3.2.3. The theory is applicable to standard photographic or video cameras, as well as to the wearable camera and personal imaging system.
Homometric Imaging and the Wyckoff principle The special case of the theory presented here in Section 3.2.1 pertains to a camera fixed camera (e.g. as one would encounter in mounting the camera on tripod). Clearly this is not directly applicable to the wearable camera system, except perhaps in the case of images acquired in very rapid succession. However, this theory, when combined with the Video Orbits theory of Section 3.2.2, is found to be useful in the context of the personal imaging system, as will be described in Section 3.2.3.
Fully automatic methods of seamlessly combining differently exposed pictures to extend dynamic range have been proposed[25][26], and are summarized here.
Most everyday scenes have a far greater dynamic range than can be recorded on a photographic film or electronic imaging apparatus (whether it be a digital still camera, consumer video camera, or eyeglass-based personal imaging apparatus as described in this paper). However, a set of pictures, that are identical except for their exposure, collectively show us much more dynamic range than any single picture from that set, and also allow the camera's response function to be estimated, to within a single constant scalar unknown.
A set of functions,
I_n(x)=f(k_n q(x)),
where 
are scalar constants,
is known as a Wyckoff setmannicip[15],
and describes a set of images, 
, when 
is the spatial coordinate of a piece of film
or the continuous spatial coordinates of the focal plane of an
electronic imaging array,
q is the quantity of light falling on the sensor array,
and f is the unknown nonlinearity of the camera's response function
(assumed to be invariant to 
.
Because of the effects of noise (quantization noise, sensor noise, etc.), in practical imaging situations, the dark (``underexposed'') pictures show us highlight details of the scene that would have been overcome by noise (e.g. washed out) had the picture been ``properly exposed''. Similarly, the light pictures show us some shadow detail that would not have appear above the noise threshold had the picture been ``properly exposed''.
A means of simultaneously estimating f and , given
a Wyckoff set , has been
proposedmannist[27][15].
A brief outline of this method follows.
For simplicity of illustration (without loss of generality),
suppose that the Wyckoff set contains two pictures,
and 
, differing only
in exposure (e.g. where the second image
received k times as much light as the first).
Photographic film is traditionally characterized
by the so-called
``D logE'' (Density versus log Exposure) characteristic
curvewyckoff[29].
Similarly, in the case of electronic imaging,
we may also use logarithmic exposure units, 
,
so that one image will be K = log(k) units darker than the other:
(f^-1(I_1)) = Q = (f^-1(I_2)) - K
The existence of an inverse for f follows from
the semimonotonicity assumptionmannicip[15].
(We expect any reasonable camera to provide a semimonotonic
relation between quantity of light received, q, and
the pixel value reported.) Since the logarithm function is also monotonic,
the problem comes down to estimating the semimonotonic function
and the scalar constant
K, given two pictures 
and 
:
The unknowns (F and K) may be solved by regression (e.g. in a typical imaging situation with 480 by 640 by 256 grey values, this amounts to solving 307200 equations in 257 unknowns: 256 for F and one for K). An intuitive way to solve this problem, which also provides valuable insight into how to combine the differently exposed images into a single image of extended dynamic range, is as follows: recognize that
provides a recipe for ``registering'' (appropriately
lightening or darkening)
the second image with the first.
This registration procedure differs from
image registration procedure commonly used
in image resolution enhancement (to be described in Section 3.2.2)
because it operates on the range (tonal range) of the image 
as opposed to its domain (spatial coordinates) .
(In Section 3.2.3, registration in both domain
and range will be addressed.)
Now if we construct a cross histogram of the two images, we will have a matrix (typically of dimension 256 by 256 assuming 8-bit-deep images) that completely captures all of the information about the relationship between the two pictures. This representation discards all spatial information in the images (which is not relevant to estimating f). Thus the regression problem (that of solving (3) can be done on the cross histogram instead of the original pair of images. This approach has the added advantage of breaking the problem down into two separate simpler steps:
,
by regarding it an
iterative map onto itself.
(See Fig8.) The
iterative map (logistic map) is most
familiar in chaos
theoryiterativemap[31],
but here,
since the map is monotonic,
the result is a deterministic function.
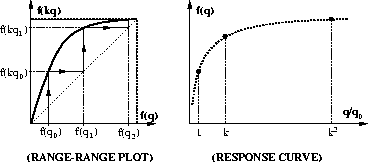
Figure 8: Procedure for finding the pointwise nonlinearity of an image
sensor from two pictures differing only in their exposures.
(RANGE-RANGE PLOT) Plot of pixel values in one
image against corresponding
pixel values in the other.
(RESPONSE CURVE) Points on the response
curve, found from only the two pictures, without
any knowledge about the characteristics of
the image sensor. These discrete points are
only for illustrative purposes.
If a logarithmic exposure
scale is used, (as most photographers do) then
the points fall
uniformly on the 
axis.
The function g is called the `range-range' plot, as it is a plot of the range of the function f(q) against the the range of the function f(kq). Separating the process into two stages also allows us a more direct route to ``registering'' the image domains, if for example, we do not need to know f, but only require a recipe for expressing the range of f(kq) in the units of f(q).
The above method allows us to estimate, to within a constant scale factor, the photometric response function of the camera without making any assumptions on the form of f, other than semimonotonicity. However, if we use a parametric model (e.g. to fit a smooth parameterized curve through the cross histogram), then the results can be somewhat more noise-immune.
A suitable parameterization is motivated by the fact that
the ``D log E'' curve of most typical photographic emulsions is linear
over a relatively wide region, which suggests the commonly used empirical
law for the response function of film [28]:
This formulation has been found to apply well to the eyeglass-based
camera system designed and built by the author.
The constant 
that
characterizes the density of unexposed film,
applies equally well to the electronic imaging array
in the eyeglass-based camera. The quantity
may be subtracted off, either
through design and adjustment of the circuits connected to the
sensor array, or through the capture of
one picture (or several pictures signal-averaged)
taken with the lens covered,
to be subtracted from each of the incoming pictures, or
it may be estimated (e.g. treated
as an additional unknown parameter).
The range-range plot
then takes the form
where k is the ratio of exposures relating the two pictures.
Thus to find the value of the linear constant, 
,
in 
we simply apply linear regression
to points in the joint histogram.
From we can obviously find the
camera's contrast parameter, 
.
Once f is determined, each picture becomes a different estimate of the same
q_n = 1k_nf^-1(I_n)
true quantity of light falling on each pixel of the image sensor. Thus one may regard each of these measurements (pixels) as a light meter (sensor element) that has some nonlinearity followed by a quantization to a measurement having typically 8-bit precision.
It should be emphasized that most image processing algorithms
incorrectly assume that the camera response function is linear
(e.g. almost all current image processing, such as blurring, sharpening,
unsharp masking, etc., operates linearly on the image)
while in fact it is seldom linear.
Even Stockham's homomorphic filteringstockham,
which advocates taking the log, applying linear filtering,
and then taking the antilog,
fails to capture the correct
nonlinearitymannpithesis[27], as it ignores
the true nonlinearity of the sensor array.
It has recently
been shownmannicip[15] that, in the absence
of any knowledge of the camera's nonlinearity, simply selecting
a value of two or three,
and using (5) to linearize the
image (e.g. square or cube all pixel values in the image),
followed by filtering, followed by the inverse operation
(e.g. extracting the square root or
cube root of each pixel in the image) provides much better results
than the approach advocated by Stockham.
Of course, finding the true response function of the camera allows
us to do even better, as we may then apply our linear signal processing
methodology to the original light falling on the image sensor.
Video Orbits
A useful assumption in the domain of `personal imaging',
is that of zero parallax, whether this
be for obtaining a first-order
estimate of the yaw, pitch, and roll of the wearer's
headmannicassp97,
or making an
important first step in the more difficult problem of
estimating depth and structure from a
scene.
Thus, in this section, the assumption is that
most of the image motion arises from
that of generating an environment map, zero-parallax
is assumed.
The problem of assembling multiple pictures of the same scene into a single image commonly arises in mapmaking (with the use of aerial photography) and photogrammetry[39], where zero-parallax is also generally assumed. Many of these methods require human interaction (e.g. selection of features), and it is desired to have a fully automated system that can assemble images from the eyeglass-based camera. Fully automatic featureless methods of combining multiple pictures have been previously proposed[40][41], but with an emphasis on subpixel image shifts; the underlying assumptions and models (affine, and pure translation, respectively) were not capable of accurately describing more macroscopic image motion. A characteristic of video captured from a head-mounted camera is that it tends to have a great deal more macroscopic image motion, and a great deal more perspective `cross-chirping' between adjacent frames of video, while the assumptions of static scene content and minimal parallax are still somewhat valid. This assumption arises for the following reasons:
.
Accordingly, two featureless methods of estimating the parameters of a projective group of coordinate transformations were first proposed inmannist, and in more detail inmannicip, one direct and one based on optimization (minimization of an objective function). Although both of these methods are multiscale (e.g. use a coarse to fine pyramid scheme), and both repeat the parameter estimation at each level (to compute the residual errors), and thus one might be tempted to call both iterative, it is preferable to refer to the direct method as repetitive to emphasize that does not require a nonlinear optimization procedure such as Levenberg-Marquardt, or the like. Instead, it uses repetition with the correct law of composition on the projective group, going from one pyramid level to the next by application of the group's law of composition. A method similar to the optimization-method was later proposed inmannicip[43]. The direct method has also been subsequently described in more detailmanntip338.
The direct featureless method for estimating the 8 scalar
parameters,
of an exact projective (homographic) coordinate transformation
is now described. In the context of personal imaging, this result is
used to multiple images to seamlessly
combine images of the same scene or object, resulting in a single
image (or new image sequence) of greater resolution or spatial extent.
Many papers have been published on the problems of motion estimation and frame alignment. (For review and comparison, seebarron95.) In this Section the emphasis is on the importance of using the ``exact'' 8-parameter projective coordinate transformationmanntip338, particularly in the context of the head-worn miniature camera.
The most common assumption (especially in motion estimation for coding, and optical flow for computer vision) is that the coordinate transformation between frames is translation. Tekalp, Ozkan, and Sezan [41] have applied this assumption to high-resolution image reconstruction. Although translation is less simpler to implement than other coordinate transformations, it is poor at handling large changes due to camera zoom, rotation, pan and tilt.
Zheng and Chellappa [46] considered the image registration problem using a subset of the affine model -- translation, rotation and scale. Other researchers [40][47] have assumed affine motion (six parameters) between frames.
The only model that properly captures the ``keystoning'' and ``chirping'' effects of projective geometry is the projective coordinate transformation. However, because the parameters of the projective coordinate transformation had traditionally been thought to be mathematically and computationally too difficult to solve, most researchers have used the simpler affine model or other approximations to the projective model.
The 8-parameter pseudo-perspective model [34] does, in fact, capture both the converging lines and the chirping of a projective coordinate transformation, but not the true essence of projective geometry.
Of course, the desired ``exact'' eight parameters come from the projective group of coordinate transformations, but they have been perceived as being notoriously difficult to estimate. The parameters for this model have been solved by Tsai and Huang [48], but their solution assumed that features had been identified in the two frames, along with their correspondences. The main contribution of the result summarized in this Section is a simple featureless means of automatically solving for these 8 parameters.
A group is a set upon which there is defined an associative law of composition (closure, associativity), which contains at least one element (identity) who's composition with another element leaves it unchanged, and for which every element of the set has an inverse.
A group of operators together with a set of operands
form a so-called group operation.
In the context of this paper,
coordinate transformations are the operators (group),
and images are the operands (set). When the coordinate transformations
form a group, then two such coordinate transformations, 
and 
, acting in succession, on an image (e.g.
acting on the image by doing a coordinate
transformation, followed by a further coordinate transformation corresponding
to , acting on that result) can be replaced by a single
coordinate transformation. That single coordinate transformation is
given by the law of composition in the group.
The orbit of a particular element of the set, under the group operation [49] is the new set formed by applying to it, all possible operators from the group.
Thus the orbit is a collection of pictures formed from one picture
through applying all possible projective coordinate transformations to that
picture. This set is referred to as the `video orbit' of the picture in
questionmanntip338.
Equivalently, we may imagine a static scene, in which the wearer of
the personal imaging system is standing at a single fixed location.
He or she generates a family of images in the same orbit of
the projective group by looking around (rotation of the
head).
The projective group of coordinate transformations,
x^ =
[ \! \!
\! \!
]
=
A[x,y]^T+bc^T [x,y]^T+1
=
Ax+bc^T x+1
is represented by 
matrices of
the form:
Where, in practical engineering problems, in which d is never
zero, the eight scalar
parameters are denoted by 
, 
, 
, and 
.
The `video orbit' of a given 2-D frame is defined to be the set of all images that can be produced by applying operators from the 2-D projective group of coordinate transformations (8) to the given image. Hence, the problem may be restated: Given a set of images that lie in the same orbit of the group, find for each image pair, that operator in the group which takes one image to the other image.
If two frames of the
video image sequence, say, 
and 
, are in the same orbit, then there
is an group operation 
such that the mean-squared error (MSE)
between and 
is zero. In practice, however,
the element of the group that takes one image ``nearest'' the
other is found (e.g. there will be a certain amount of
error due to violations in the assumptions, due to
noise such as
parallax, interpolation error, edge effects, changes in lighting, depth of
focus, etc).
The brightness constancy constraint equation [51] which gives the flow velocity components, is:
As is well-known [51]
the optical flow field in 2-D is under constrained
The model of pure
translation at every point has two parameters, but there is only one
equation (10) to solve, thus
it is common practice to compute the optical flow over some
neighborhood, which must be at least two pixels, but is generally
taken over a small block, 
, 
, or
sometimes larger (e.g. the entire image, as in the
Video Orbits algorithm described here).
However, rather than estimating the 2 parameter translational flow, the task here is to estimate the eight parameter projective flow (8) by minimizing:
_flow=(u_m^TE_x + E_t)^2
Although a sophisticated nonlinear optimization procedure, such as Levenberg-Marquardt, may be applied to solve (11), it has been found that solving a slightly different but much easier problem, allows us to estimate the parameters more directly and accurately for a given amount of computationmanntip338:
_w=((Ax+b-(c^Tx+1)x)^TE_x+(c^Tx+1)E_t)^2
(This amounts to weighting the sum differently.)
Differentiating (eq:nonlinearopt) with respect to the free
parameters 
,
and setting the result to zero gives a linear solution:
( ^T ) [a_11,a_12,b_1,a_21,a_22,b_2,c_1,c_2]^T
= (x^TE_x-E_t)
where 
In practice, this process has been improved significantlymannpithesis[25] by using an `Abelian pre-processing step' based on generalizations of Fourier transform cross spectra [52], such as the cross-Fourier-Mellin transform [53] and subspaces of the cross-chirplet transformmannws, as well as non-commutative subgroup pre-processing based on the full cross-chirplet transform which is a generalization of the multi-resolution Fourier transform [55][56].
Dynamic Range and `Dynamic Domain'
The contribution of
this Section is a simple method of ``scanning'' out a scene, from
a fixed point in space, by panning, tilting, or rotating
a camera, whose
gain (automatic exposure, electronic level control,
automatic iris, AGC, or the
like
)
is also allowed to change of its own accord (e.g. arbitrarily).
Nyquist showed how a signal can be reconstructed from a sampling of finite resolution in the domain (e.g. space or time), but assumed infinite dynamic range (e.g. infinite precision or word length per sample). On the other hand, if we have infinite spatial resolution, but limited dynamic range (even if we have only 1 bit of image depth), Curtis and Oppenheim [57] showed that we can also obtain perfect reconstruction using an appropriate modulation function. In the case of the personal imaging system, we typically begin with images that have very low spatial resolution and very poor dynamic range (video cameras tend to have poor dynamic range, and this poor performance is especially true of the small CCDs that the author uses in constructing unobtrusive lightweight systems). Thus, since we lack both spatial and tonal resolution, we are not at liberty to trade some of one for more of the other. Thus the problem of `spatiotonal' (simultaneous spatial and tonal) resolution enhancement is of particular interest in personal imaging.
In Section 3.2.1, a new method of allowing a camera to self-calibrate was proposed. This methodology allowed the tonal range to be significantly improved. In Section 3.2.2, a new method of resolution enhancement was described. This method allowed the spatial range to be significantly enhanced.
In this Section (3.2.3), a method of enhancing both the tonal range and the spatial domain resolution of images is proposed. It is particularly applicable to processing video from miniature covert eyeglass-mounted cameras, because it allows very noisy low quality video signals to provide not only high-quality images of great spatiotonal definition, but also to provide a rich and accurate photometric measurement space which may be of significant use to intelligent signal processing algorithms. That it provides not only high quality images, but also linearized measurements of the quantity of light arriving at the eyeglasses from each possible direction of gaze, follows from a generalization of the photometric measurement process outlined in Section 3.2.1.
Most notably, this generalization of the method no longer assumes that the camera need be mounted on a tripod, but only that the images fall in the same orbit of a larger group, called the `projectivity+gain' group of transformations.
Thus the apparatus can be easily used without
conscious thought or effort, which gives rise to new intelligent
signal processing capabilities.
The method works as follows:
As the wearer of the apparatus looks around, the portion of the
field of view that controls the gain (usually the central region
of the camera's field of view) will be pointed toward different objects
in the scene. Suppose for example, that the wearer is looking
at someone so that their face is centered in the frame of the camera,
. Now suppose that the wearer tips his or her head upward so
that the camera is pointed at a light bulb up on the ceiling,
but that the person's face is still visible at the bottom of the
frame, . Because the light bulb has moved into the center of
the frame, the camera's
AGC causes the entire image to darken significantly.
Thus these two images, which both contain the face of the person
the wearer is talking to, will be very differently exposed.
When registered in the spatial sense (e.g. through the appropriate
projective coordinate transformation), they will be identical, over
the region of overlap, except for exposure,
if we assume that the
wearer swings his or her head around quickly
enough to make any movement in the person he is talking to negligible.
While this
assumption is not always true, there are certain times that it is true
(e.g. when the wearer swings his or her head quickly from left to right
and objects in the scene are moving relatively slowly).
Because the algorithm can tell when the assumptions are true (by
virtue of the error), during the times it is true, it use
the multiple estimates of 
, the quantity of light received,
to construct a high definition environment map.
An example of an image sequence captured with a covert eyeglass-based version of the author's WearComp7, and transmitted wirelessly to the Internet, appears in Fig 9.
Figure 9: The `fire-exit' sequence, taken using an eyeglass-based
personal imaging system embodying AGC.
(a)-(j) frames 10-19:
as the camera pans across to take in more of the
open doorway, the image brightens up showing more of the
interior, while, at the same time, clipping highlight detail.
Frame 10 (a) shows the writing on the white paper taped to the
door very clearly, but the interior is completely black.
In frame 15 (f) the paper is completely obliterated -- it is
so ``washed out'' that we cannot even discern that there is a paper
present. Although the interior is getting brighter,
it is still not discernible in frame 15 (f),
but more and more detail of the interior becomes visible
as we proceed through the sequence,
showing that the fire exit is blocked by the clutter inside.
(A)-(J) `certainty' images (as described
in Section 3.2.3) corresponding to (a)-(j) indicate the
homometric step size. (Bright areas indicate regions of the
image which are midtones, and hence have greater
homometric certainty, while dark
areas of the certainty image indicate regions falling in
either the shadows or highlights, and are therefore
have lesser homometric certainty.)
Clearly, in this application, AGC, which has previously been regarded as a serious impediment to machine vision and intelligent image processing, becomes an advantage. By providing a collection of images with differently exposed but overlapping scene content, additional information about the scene, as well as the camera (information that can be used to determine the camera's response function, f) is obtained. The ability to have, and even benefit from AGC is especially important for WearCam contributing to the hands-free nature of the apparatus, so that one need not make any adjustments when, for example, entering a dimly lit room from a brightly lit exterior.
`Spatiotonal' processing, as it is calledmannpithesis, extends the concept of motion estimation to include both `domain motion' (motion in the traditional sense) as well as `range motion' (Fig 10),
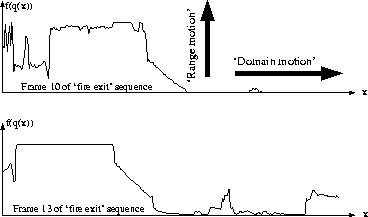
Figure 10:
One row across each of two images from the `fire exit' sequence.
`Domain motion' is motion in the traditional sense
(e.g. motion from left to right, zoom, etc.), while
`Range motion' refers to a tone-scale adjustment
(e.g. lightening or darkening of the image).
In this case, the camera is panning to the right,
so domain motion is to the left. However, when panning
to the right, the camera points more and more into the darkness
of an open doorway, causing the AGC to adjust the exposure.
Thus there is some ``upwards'' motion of the curve as well
as ``leftwards'' motion. Just as panning the camera
across causes information to leave the
frame at the left, and new information to enter at the right,
the AGC causes information to leave from the top (highlights
get clipped)
and new information to enter from the bottom (increased
shadow detail).
and proceeds as follows:
As in[27], consider one dimensional ``images'' for
purposes of illustration, with the understanding that the actual
operations are performed on 2-D images.
The 1-D projective+gain group is defined in terms of the
``group''
of projective coordinate transformations, taken together with the
one-parameter group of gain (image darkening/lightening) operations:
p_a,b,c,k f(q(x)) = g_k(f(q(ax+bcx+1))) = f(kq(ax+bcx+1))
where 
characterizes the gain operation,
and admits a group representation:
[
],
giving the law of composition:
where the first law of composition on the right hand side is the usual
one for the projective group (a subgroup of the projective+gain
group), and the second one is that of the
one-parameter gain (homometric lightening/darkening) subgroup.
Two successive frames of a video sequence are related through a group-action that is near the identity of the group, thus one may think of the Lie algebra of the group as providing the structure locally. As in previous work[26] an approximate model which matches the `exact' model in the neighbourhood of the identity is used.
For the `gain group' (which is a one parameter group isomorphic to
addition over the reals, or multiplication over the positive reals),
the approximate model
may be taken from Eq 5, by noting that:
g(f(q)) = f(kq) = + (kq)^
= - k^+ k^+ k^q^
Thus we see that g(f) is a ``linear equation'' (is affine) in f.
This affine relationship
suggests that linear regression on the cross histogram between
two images would provide an estimate of and , while
leaving 
unknown, which is consistent with the fact that the response
curve may only be determined up to a constant scale factormann384.
From (16)
we have that the (generalized) brightness change constraint equation is:
.
where F(x,t)=f(q(x,t)).
Combining this equation with the Taylor series
representation:
where 
, at time t,
and 
is the frame difference of adjacent frames,
we have:
Thus, the brightness change constraint equation becomes:
where, normalizing, 
.
Substitution of an approximate model (quadratic Taylor series)
into (19) gives:
as the non-weighted solution,
where 
, 
, and 
.
Minimizing 
yields a linear solution in parameters of the approximate model:
where F(x,t)=f(q(x)) at time t, , at time t,
and is the frame difference of adjacent frames.
To construct a single floating-point image of increased spatial extent and increased dynamic range, first the images are spatiotonally registered (brought not just into register in the traditional `domain motion' sense, but also brought into the same tonal scale through homometric gain adjustment). This form of spatiotonal transformation is illustrated in Fig 11 where all the images are transformed into the coordinates of the first image of the sequence, and in Fig 12 where all the images are transformed into the coordinates of the last frame in the image sequence. It should be noted that the final homometric composite can be made in the coordinates of any of the images. The choice of reference frame is arbitrary since the result is a floating point image array (not quantized)! Furthermore, the final composite need not even be expressed in the spatiotonal coordinates of any of the incoming images. For example homometric coordinates (linear in the original light falling on the image array) may be used, to provide an array of measurements that linearly represent the quantity of light, to within a single unknown scalar constant for the entire array.
Figure 11: All images expressed in the
spatiotonal coordinates of the first image in the sequence.
Note both the ``keystoning'', or ``chirping'' of the images
toward the end of the sequence, indicating the spatial
coordinate transformation, as well as the darkening,
indicating the tone scale adjustment, both of which make
the images match (a).
Prior to quantization for printing in this figure,
the darker images (e.g. (i) and (j)) contained a tremendous
deal of shadow detail, owing to the fact that the homometric
step sizes are much smaller when compressed into the domain
of image (a).
Figure 12: All images expressed in spatiotonal coordinates of the last
image in the sequence. Before re-quantization to print this
figure, (a) had the highest level of highlight detail,
owing to is very small homometric quantization step size
in the bright areas of the image.
Once spatiotonally registered, each pixel of the output image is constructed from a weighted sum of the images whose coordinate-transformed bounding boxes fall within that pixel. The weights in the weighted sum are the so-called `certainty functions', which are found by evaluating the derivative of the corresponding estimated effective ``characteristic function'' at the pixel value in question[58].
Although the response function, f(q),
is fixed for a given camera, the `effective response function',
depends on the exposure, 
, associated with frame, i,
in the image sequence. By evaluating 
, we arrive
at the so-called `certainty images' (Fig 9).
Lighter areas of the `certainty images' indicate moderate values of
exposure (mid-tones in the corresponding images), while darker values
of the certainty images designate exposure extrema -- exposure in the
toe or shoulder regions of the response curve
where it is difficult to discern subtle differences in exposure.
The composite image may be explored interactively on a computer system (Fig 13).
Figure 13: Virtual camera:
Floating point projectivity+gain image composite
constructed from the
fire-exit sequence. The dynamic range of the image is far
greater than that of a computer screen or printed page.
The homometric information
may be interactively viewed on the computer screen, however,
not only as an environment map (with pan, tilt, and zoom),
but also with control of `exposure' and contrast.
This makes the personal imaging apparatus into a telematic camera in which viewers on the World Wide Web experience something similar to a QuickTime VR environment mapquicktime, except with some new additional controls allowing them to move around in the environment map both spatially and tonally.
It should be noted that the environment map was generated by a covert wearable apparatus, simply by looking around, and that no special tripod or the like was needed, nor was there significant conscious thought or effort required. In contrast to this proposed method of building environment maps, consider what must be done to build an environment map using QuickTime VR:
Despite more than twenty years photographic experience, Charbonneau needed to learn new approaches for this type of photography. First, a special tripod rig is required, as the camera must be completely level for all shots. A 35 mm camera ... with a lens wider than 28 mm is best, and the camera should be set vertically instead of horizontally on the tripod. ... Exposure is another key element. Blending together later will be difficult unless identical exposure is used for all views.quicktimeThe constraint of the QuickTime VR method and many other methods reported in the literatureszeliski[36][38], that all pictures be taken with identical exposure, is undesirable for the following reasons:
Once the final image composite, which reports, up to a single unknown scalar, the quantity of light arriving from each direction in space, it may also be reduced back to an ordinary (e.g. non-homometric) picture, by evaluating it with the function f. Furthermore, if desired, prior to evaluating it with f, a lateral inhibition similar to that of the human visual system, may be applied, to reduce its dynamic range, so that it may be presented on a medium of limited display resolution, such as a printed page (Fig 14).
Figure 14: Fixed-point image made by
tone-scale adjustments that are only locally monotonic,
followed by quantization to 256 greylevels.
Note that we can see clearly both the small piece of white paper on
the door (and even
read what it says -- ``COFFEE HOUSE ''),
as well as the details of the dark interior.
Note that we could not have captured such a nicely exposed
image using an on-camera ``fill-flash'' to reduce scene
contrast, because the fill-flash would mostly light
up the areas near the camera (which happen
to be the areas that are already too bright), while
hardly affecting objects at the end of the dark corridor
which are already too dark. Thus, one would need to
set up additional photographic lighting equipment
to obtain a picture of this quality. This image
demonstrates the advantage
of a small lightweight personal imaging system,
built unobtrusively into a pair of eyeglasses, in that
an image of very high quality was captured by simply
looking around, without entering the corridor.
This might
be particularly useful if trying to report a violation of
fire-safety laws, while at the same time, not appearing
to be trying to capture an image.
Note that this image was shot from some distance away from
the premises (using a miniaturized tele lens
I built into my eyeglass-based system) so that the effects
of perspective, although still present, are not as
immediately obvious as with some of the other extreme
wide-angle image composites presented in this thesis.
The success of the covert, high definition
image capture device suggests possible
applications in investigative journalism,
or simply to allow
ordinary citizens to report violations of fire safety
without alerting the perpetrators.
It should be noted that this homometric filtering
process (that of
producing 14)
would reduce to a variant of homomorphic filtering, in the case
of a single image, ,
in the sense that I would be treated to
a global nonlinearity 
(to obtain q) then linearly processed
(e.g. with unsharp masking or the like),
and then the nonlinearity, would be undone, by
applying f:
I_c = f(L(f^-1(I)))
where 
is the output (or composite) image and
L is the linear filtering operation.
Images sharpened in this way tend to have a much richer, more
pleasing and natural appearancemannpithesis, than those
that are sharpened according to either a linear filter,
or the variant of homomorphic filtering suggested by Stockhamstockham.
Perhaps the greatest value of homometric imaging, apart from its ability to capture high quality pictures that are visually appealing, is its ability to measure the quantity of light arriving from each direction in space. In this way, homometric imaging turns the camera into an array of accurate light meters.
Furthermore, the process of making these measurements is activity driven in the sense that areas of interest in the scene will attract the attention of the human operator, so that he or she will spend more time looking at those parts of the scene. In this way, those parts of the scene of greatest interest will be measured with the greatest assortment of ``rulers'' (e.g. with the richest collection of differently quantized measurements), and will therefore, without conscious thought or effort on the part of the wearer, be automatically emphasized in the composite representation. This natural foveation process arises, not because the Artificial Intelligence (AI) problem has been solved and built into the camera, so that it knows what is important, but simply because the camera is using the operator's brain as its guide to visual saliency. Because the camera does not take any conscious thought or effort to operate, it ``lives'' on the human host without presenting the host with any burden, yet it benefits greatly from this form of humanistic intelligence.
Bi-foveated WearCam The natural foveation, arising from the symbiotic relationship between human and machine (humanistic intelligence) described in Section 3.2.3 may be further accentuated by building a camera system that is itself foveated.
Accordingly, the author designed and built a number of WearComp embodiments containing more than one electronic imaging array. One common variant, with a wide-angle camera in landscape orientation combined with a telephoto camera in portrait orientation was found to be particularly useful for humanistic intelligence: The wide camera provided the overall contextual information from the wearer's perspective, while the other (telephoto) provided close-up details, such as faces.
This `bi-foveated' scheme was found to work well within the context of the spatiotonal model described in the previous Section (3.2.3).
One realization of the apparatus comprised two cameras concealed in a pair of ordinary eyeglasses, is depicted in Figure 15.
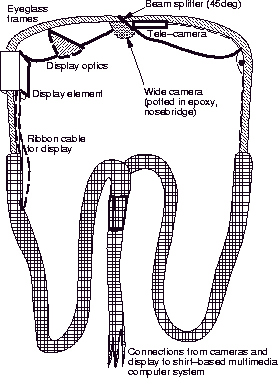
Figure 15: A multicamera personal imaging system
with two miniature cameras and display
built into ordinary eyeglasses. This bi-foveated scheme
was found to be useful in a host of applications ranging from
crime-reduction (personal safety/personal documentary),
to situational awareness and shared visual memory.
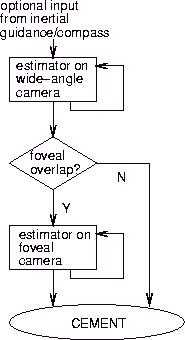
Figure 16: Signal processing approach for bi-foveated `WearCam'.
Note also that the spatial coordinates are propagated according
to the projective group's law of composition while the gain
parameters between the wide-camera and foveal-camera are
not directly coupled.
Signal processing with respect to bi-foveated cameras is a special consideration. In particular, since the geometry of one camera is fixed (in epoxy or the like) with respect to the other, there exists a fixed coordinate transformation that maps any image captured on the wide camera to one that was captured on the foveal camera at the same time. Thus when there is a large jump between images captured on the foveal camera -- a jump too large to be considered in the neighbourhood of the identity -- signal processing algorithms may look to the wide camera for a contextual reference, owing to the greater overlap between images captured on the wide camera, apply the estimation algorithm to the two wide images, and then relate these to the two foveal images. Furthermore, additional signal inputs may be taken from miniature wearable radar systems, inertial guidance, or electronic compass, built into the eyeglasses or clothing. These extra signals typically provide ground-truth, as well as cross-validation of the estimates reported by the proposed algorithm. The procedure (described in more detail inmannicassp97) is illustrated in Fig 16.
Lightspace modeling for H.I.
The result of homometric imaging is that, with
the appropriate signal processing, WearComp can measure
the quantity of light arriving from each angle in space.
Furthermore, because it has display capability (usually
the camera sensor array and display element are both
mounted in the same eyeglass frame), it may also direct
rays of light into the eye.
Suppose that the display element has a response function h.
The entire apparatus (camera, display, and signal processing circuits)
may be used to create an `illusion of transparency',
through display of the quantity 
where is the image from the camera.
In this way, the wearer sees ``through'' (e.g. by virtue of) the
camera, and would be blind to outside objects
in the region over which the apparatus operates,
but for the camera.
Now suppose that a filter, L, is inserted into the
`reality stream' by virtue of the appropriate signal processing
on the incoming images prior to display on h:
I_m = h^-1(L(f^-1(I_c)))
In this context, L is called the `visual filter'mann260, and may be more than just a linear spatial filtering operation. As a trivial but illustrative example, consider L such that it operates spatially to flip the image left-right. This would make the apparatus behave like the left-right reversing glasses that Kohlerkohler64 and Dolezaldolezal82 made from prisms for their psychophysical experiments. (See Fig 17 (VR).)
Figure 17:
Lightspace modeling:
The WearComp apparatus, with the appropriate
homometric signal processing, may be thought of as
a hypothetical glass that absorbs
and quantifies every ray of
light that hits it, and is also capable of generating
any desired bundle of rays of light coming out the other side.
Such a glass, made into a visor, could produce a
virtual reality (VR) experience by ignoring
all rays of light from the real world, and generating
rays of light that simulate a virtual world.
Rays of light from real (actual) objects
indicated by solid shaded lines; rays of light from
the display device itself indicated by dashed lines.
The device could also produce a typical
augmented reality (AR)feiner93[63]
experience by creating the
`illusion of transparency'
and also generating rays of
light to make computer-generated ``overlays''.
Furthermore, it could `mediate' the visual experience,
allowing the perception of reality itself to be altered.
In this figure, a simple but illustrative example is shown:
objects are left-right reversed before being presented
to the viewer.
In general, through the appropriate selection of L, the perception of visual reality may be augmented, deliberately diminished (e.g. to emphasize certain objects by diminishing the perception of all but those objects), or otherwise altered.
One feature of this wearable tetherless computer-mediated reality system is that the wearer can choose to allow others to alter his or her visual perception of reality over an Internet connected wireless communications channel. An example of such a shared environment maps appears in Figure 18). This map not only allows others to vicariously experience our point of view (e.g. here a spouse can see that the wearer is at the bank, and send a reminder to check on the status of a loan, or pay a forgotten bill), but can also allow the wearer to allow the distant spouse to mediate the perception of reality. Such mediation may range from simple annotation of objects in the `reality stream', to completely altering the perception of reality.
Figure 18: Shared environment maps are one obvious application of
WearComp.
Images transmitted from the author's
`Wearable Wireless Webcam'mannwearcam
may be seamlessly ``stitched'' together onto a WWW page so
that others can see a first-person-perspective
point of view, as if looking over the author's shoulder.
However,
because the communication is bidirectional, others can send
communicate with the wearer by altering the visual perception
of reality. This might, for example, allow one
to recognize people one has
never met before. Thus personal imaging allows the individual to go beyond
a cyranic [65] experience, toward a more
symbiotic relation to a networked collective humanistic
intelligence within a mediated reality environment [12].
(C) Steve Mann, 1995. Picture rendered at higher-than-normal
screen resolution for use as cover for a journal.
Other examples of computer-mediated reality include lightspace modeling, so that the response of everyday objects to light can be characterized, and thus the objects can be recognized as belonging to the same orbit of the group of transformations described in this paper. This approach facilitated such efforts as a way-finding apparatus that would prevent the wearer from getting lost, as well as an implementation of Feiner's Post-It-note metaphor using a wearable tetherless device, so that messages could be left on everyday objects.
Beyond video: Synthetic synesthesia and Personal Imaging for HI The manner in which WearComp, with its rich multidimensional measurement and signal processing space, facilitates enhanced environmental awareness, is perhaps best illustrated by way of the author's effort of the 1980s at building an system to assist the visually challenged. This device, which used radar, rather than video, as the input modality, is now described.
VibraVest for Synthetic Synesthesia
Mediated reality may include, in addition to video, an
audio reality mediator, or, more generally, a `perceptual
reality mediator'. This generalized mediated perception system
may include deliberately induced
synesthesia.
Perhaps the most interesting example
of synthetic synesthesia was
the addition of a new
human sensory capability based on miniature wearable radar systems
combined with intelligent signal processing.
In particular, the author
developed a number of vibrotactile wearable radar systems
in the 1980s,
of which there were three primary variations:
.
This provided the sensation of an extended `envelope'
around the body, in which one could feel objects at a distance.
In later (late 1980s) embodiments of `CorporealEnvelope',
envelope detection was done after splitting the signal into
three or four separate
frequency bands, each driving a separate vibrotactile
device, so that each would convey a portion of the Doppler
spectrum (e.g. each corresponding to a range of velocities of
approach).
In another late 1980s embodiment, variously colored
lamps were used, attached to the wearer's eyeglasses to
provide a visual synesthesia of the radar sense. In one particular
embodiment, red, green, and blue lamps were used, such that
objects moving toward the wearer illuminated the blue
lamp, while objects
moving away illuminated the red lamp.
Objects not moving relative to the wearer,
but located near the wearer appeared green.
This work was inspired by using the metaphor of the natural Doppler shift colors.
in real time, suggest a renewed hope for the
success of this effort to assist the visually impaired.
Such simple systems as these suggest a future in which intelligent signal processing, through the embodiment of humanistic intelligence, becomes environmentally aware. It is misleading to think of the wearer and the computer with its associated input/output apparatus as separate entities. Instead it is preferable to regard the computer as a second brain, and its sensory modalities as additional senses, which through synthetic synesthesia are inextricably intertwined with the wearer's own biological sensory apparatus.
Conclusions A new form of intelligent signal processing, called `Humanistic Intelligence' (HI) was proposed. It is characterized by processing hardware that is inextricably intertwined with a human being to function as a true extension of the user's mind and body. This hardware is constant (always on, therefore its output is always observable), controllable (e.g. is not merely a monitoring device attached to the user, but rather, it takes its cues from the user), and is corporeal in nature (e.g. tetherless and with the point of control in close proximity to the user so as to be perceived as part of body).
Furthermore, the apparatus forms a symbiotic relationship with its host (the human), in which the high-level intelligence arises on account of the existence of the host (human), and the lower-level computational workload comes from the signal processing hardware itself.
The emphasis of this paper was on Personal Imaging, to which the application of HI gave rise to a new form of intelligent camera system. This camera system was found to be of great use in both photography and documentary video making. Its success arose from the fact that it (1) was simpler to use than even the simplest of the so-called ``intelligent point and click'' cameras of the consumer market (many of which embody sophisticated neural network architectures), and (2) afforded the user much greater control than even the most versatile and fully-featured of professional cameras.
This application of HI took an important first step in moving from the `point and click' metaphor, toward the `look and think' metaphor -- toward making the camera function as a true visual memory prosthetic which operates without conscious thought or effort, while at the same time affording the visual artist a much richer and complete space of possibilities.
A focus of HI was to put the human intellect into the loop but still maintain facility for failsafe mechanisms operating in the background. Thus the personal safety device, which functions as a sort of ``black box'' monitor, was suggested.
What differentiates H.I. from environmental intelligence (ubiquitous computingweiser, reactive roomscooperstock, and the like, is that there is no guarantee environmental intelligence will be present when needed, or that it will be in control of the user. Instead, H.I. provides a facility for intelligent signal processing that travels with the user. Furthermore, because of the close physical proximity to the user, the apparatus is privy to a much richer multidimensional information space than that obtainable by environmental intelligence.
Furthermore, unlike an intelligent surveillance camera that people attempt to endow with an ability to recognize suspicious behaviour, WearComp takes its task from the user's current activity, e.g. if the user is moving, it's taking images, if the user is still it's not taking in new orbits based on the premise that the viewpoint changes, etc.
Systems embodying H.I. are:
Acknowledgements The author wishes to thank Simon Haykin, Rosalind Picard, Steve Feiner, Charles Wyckoff, Hiroshi Ishii, Thad Starner, Jeffrey Levine, Flavia Sparacino, Ken Russell, Richard Mann, and Steve Roberts (N4RVE), for much in the way of useful feedback, constructive criticism, etc., as this work has evolved, and Zahir Parpia for making some important suggestions for the presentation of this material. Thanks is due also to individuals the author has hired to work on this project, including Nat Friedman, Chris Cgraczyk, Matt Reynolds (KB2ACE), etc., who each contributed substantially to this effort.
Dr. Carter volunteered freely of his time to help in the design of the interface to WearComp2 (the author's 6502-based wearable computer system of the early 1980s), and Kent Nickerson similarly helped with some of the miniature personal radar units and photographic devices involved with this project throughout the mid 1980s.
Much of the early work on biosensors and wearable computing was done with, or at least inspired by work the author did with Dr. Nandegopal Ghista, and later refined with suggestions from Dr. Hubert DeBruin, both of McMaster University. Dr. Max Wong of McMaster university supervised a course project in which the author chose to design an RF link between two 8085-based wearable computers which had formed part of the author's ``photographer's assistant'' project.
Much of the inspiration towards making truly wearable (also comfortable and even fashionable) signal processing systems was inspired through collaboration with Jeff Eleveld during the early 1980s.
Bob Kinney of US Army Natick Research Labs assisted in the design of a tank top, based on a military vest, which the author used for a recent (1996) embodiment of the WearComp apparatus worn underneath ordinary clothing.
Additional Thanks to VirtualVision, HP labs, Compaq, Kopin, Colorlink, Ed Gritz, Miyota, Chuck Carter, and Thought Technologies Limited for lending or donating additional equipment that made these experiments possible.